Límite de Shockley-Queisser de las Células Solares Fotovoltaicas

Si eres un profesional del sector fotovoltaico estarás familiarizado con el concepto de eficiencia de una célula fotovoltaica y cómo todos los fabricantes de paneles solares del mundo se esfuerzan en publicar sus logros en cuanto a "récords" de eficiencia. Sin embargo, en este artículo vamos a ver que existe un límite físico a la eficiencia máxima teórica de una célula solar que difícilmente se puede superar, llamado límite de Shockley-Queisser. Además de sus posibles desafíos y mejoras para poder incrementar ligeramente este límite.

¿Qué es el Límite de Shockley-Queisser?

El límite de Shockley-Queisser es el máximo teórico de eficiencia energética que una célula solar de unión única puede alcanzar bajo iluminación solar estándar. Este límite, establecido por William Shockley y Hans Queisser en 1961, se basa en principios de la termodinámica y la física del estado sólido.

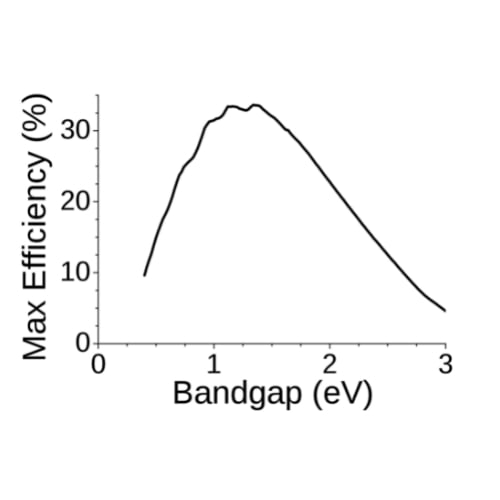
¿Qué factores se consideran para calcular este límite?

Factores como el espectro solar, las propiedades de absorción del material semiconductor utilizado y la recombinación de electrones y huecos generados por la luz solar. El límite teórico máximo de eficiencia para una célula solar de unión única es aproximadamente el 33.7% bajo condiciones de un sol (AM1.5). Esto quiere decir, que, como máximo 337W/m2 de la energía solar incidente se podría convertir en electricidad.

¿Qué es AM1.5 y por qué se utiliza para calcular el límite de Shockley-Queisser?

El término AM1.5 se refiere a la "Masa de Aire 1.5" y es un estándar utilizado para la medición de la radiación solar en la superficie terrestre.

¿Por qué es importante AM1.5 en el contexto de las células solares para calcular el límite de Shockley-Queisser?

Porque proporciona una referencia consistente para evaluar el rendimiento de las células solares bajo condiciones que simulan la luz solar real en una gran cantidad de lugares de la Tierra.

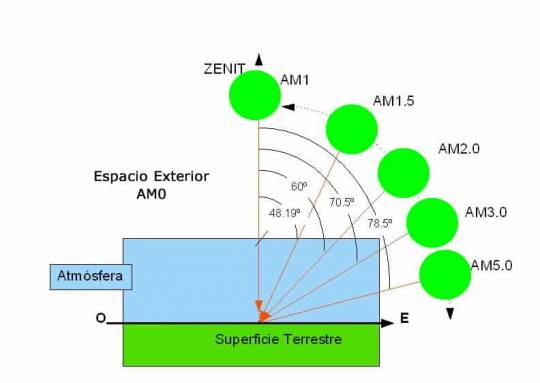
La masa de aire (AM) es una medida de la cantidad de atmósfera que la luz solar debe atravesar antes de llegar a la superficie terrestre. Cuando el sol está en su punto más alto en el cielo (en el zenit), la masa de aire es 1 (AM1).

Sin embargo, cuando el sol está a 48.2 grados del cenit, la luz solar atraviesa una cantidad de atmósfera 1.5 veces mayor que en el cenit, de ahí el término AM1.5.

El espectro AM1.5 es el elegido para la estandarización de pruebas de eficiencia de células solares, ya que representa las condiciones de iluminación promedio encontradas en muchas partes del mundo.

Este estándar se utiliza para proporcionar una base común para comparar el rendimiento de diferentes tecnologías fotovoltaicas.

¿Cómo se obtiene el Límite de Shockley-Queisser?

El cálculo del límite de Shockley-Queisser se calcula del siguiente modo:

Radiación del cuerpo negro:

Cuando los objetos negros, o cuerpos negros, se calientan, para evitar calentarse "hasta el infinito", liberan esa energía en forma de radiación.

Las células de los paneles solares son de color oscuro y suelen estar recubiertas de un material antirreflectante que les permite captar mejor la luz incidente. Pero parte de esta luz es absorbida por el material oscuro (la célula) y liberada por la radiación de cuerpo negro. Esto significa aproximadamente el 7% de la energía disponible para la célula solar.

La radiación de cuerpo negro (radiación electromagnética de un cuerpo en equilibrio termodinámico con su entorno) de una célula solar a temperatura ambiente (300 K = 25ºC) no puede ser captada por la célula, y representa aproximadamente el 7% de la energía entrante disponible.

Además, toda la energía que no se convierte en electricidad suele transformarse en calor. Eso significa más radiación de cuerpo negro, y más pérdida de energía.

A medida que aumenta la temperatura de las células, aumenta también la radiación del cuerpo negro, hasta que se alcanza el equilibrio.

En la práctica, este equilibrio se alcanza normalmente a temperaturas de hasta 360 K (86ºC), y las células suelen funcionar con eficiencias inferiores a su valor nominal a temperatura ambiente.

Recombinación de los electrones:

Necesitamos los electrones en la banda de conducción, porque aquí es donde pueden fluir, y es lo que produce electricidad. Los electrones, inicialmente en reposo, se almacenan en la banda de valencia. Para pasar a la banda de conducción necesita un fotón o partícula de luz de alta energía que le aporta una energía superior a la banda de la banda prohibida como se puede ver en la siguiente imagen.

La recombinación impone un límite superior a la tasa de producción de electrones-huecos, a mayor recombinación, menor producción. Esto es por que, con la recombinación, la energía del fotón que hizo desplazar un electrón de la banda de valencia a la de conducción, se desperdicia. En el silicio, esto reduce el rendimiento teórico en condiciones normales de funcionamiento en otro 10%, además de las pérdidas térmicas.

Poniendo un ejemplo, imagina que tu hermano te da un empujón, y tú aprovechando el impulso, lanzas un boomerang a un amigo que está alrededor de ti moviéndose en una bicicleta. El boomerang sería el electrón que queremos que llegue a tu amigo, tu amigo en bicicleta sería la banda de conducción y la energía de ayuda del empujón sería el fotón. Si el boomerang llega a tu amigo, sería como el electrón que fluye y genera electricidad (se mueve), si no llega y vuelve a ti, es la recombinación y se ha perdido esa energía.

La ecuación básica para el límite de Shockley-Queisser considera la tasa de generación de pares electrón-hueco por absorción de fotones y la tasa de recombinación de estos pares.

En el caso de las células comerciales, mayoritariamente de Silicio, de los 1.000 W/m² de radiación solar a AM1.5, aproximadamente el 19% tiene menos de 1,1 eV de energía y no producirá energía en una célula de silicio. Esto representa alrededor del 33% de la luz solar incidente, lo que significa que sólo por las pérdidas espectrales hay una eficiencia de conversión teórica de alrededor del 48%, ignorando todos los demás factores.

Si sumamos todas las pérdidas de cuerpo negro y de recombinación, solamente se puede aprovechar el 33,7% de la radiación incidente (337W/m2) en condiciones de AM1.5. Este es límite de Shockley-Queisser.

Se puede ver en la siguiente gráfica, como las células de Silicio realmente están ya al límite físico de eficiencia (podrían llegar al 27-28%) sin embargo, otras combinaciones de otros materiales no basadas en silicio, tienen un límite teórico superior aunque lejos de lograrse en la práctica por su incremento en los costes de fabricación.

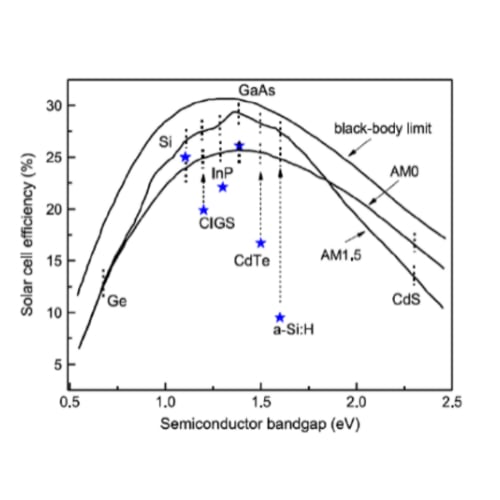
¿Se puede superar el límite de Shockley-Queisser?

Si, por supuesto, se puede superar pero utilizando células multiunión o tandem. Esto quiere decir, que son células que incorporan más de una capa de diferentes materiales e incorporan una especie de "túneles" para que los fotones puedan pasar de unas capas a otras. De este modo se pueden llegar a alcanzar eficiencias teóricas de más del 85%.

¿Cómo sería la estructura de una célula que supera el límite Shockley-Queisser?

Un buen ejemplo sería una célula tandem compuesta de fosfuro de indio y galio (InGap), arseniuro de galio (GaAs) y Germanio (Ge). Estos materiales tienen una banda prohibida de 1,86 eV, 1,4 eV y. 0,65 eV.

Esto lo que quiere decir es que el fosfuro de indio y galio necesita fotones con 1,86 eV de energía para que sus electrones pasen a la banda de conducción, el arseniuro de Galio, necesitará fotones con energía de 1,4 eV para que sus electrones pasen a la banda de conducción y el Germanio, solo 0,65 eV,

Si lo ves como una "pila" de materiales interconectados como "túneles" para flujo de fotones, la célula de InGaP/GaAs/InGaAs que tendría un comportamiento similar al InGap/GaAs/Ge y se vería así:

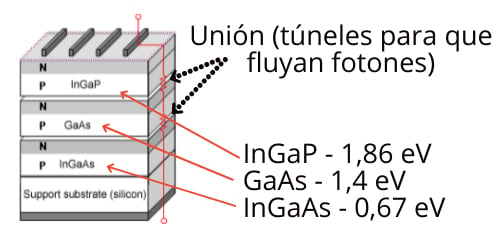
Esto lo que provoca es que cada capa de la célula aprovecha fotones con una energía útil para desplazar los electrones a su capa de conducción. Los fotones que no poseen suficiente energía para los 1,86 eV del InGap, pasarían a la siguiente capa GaAs con 1,4 eV, que es inferior a la precedente. Así sucesivamente para ir aprovechando fotones con menor energía en cada capa. De este modo, si vemos la curva espectral de la luz solar incidente de la imagen siguiente, esta célula del ejemplo va aprovechando esos niveles de energía de los fotones, de más a menos:

Esta práctica, multicapa, se podría llevar, teóricamente hasta niveles cercanos al 85% de eficiencia d conversión en una hipotética sucesión de capas de materiales con banda prohibida en escala descendente para llegar a un aprovechamiento casi total de la luz solar.

¿Qué niveles de eficiencia tienen los paneles solares actuales?

Los paneles solares comerciales que se utilizan en la actualidad, están basados en silicio, por lo que su límite máximo teórico dificilmente superará el 28% de eficiencia con células unicapa.

Los mejores paneles solares del mercado están rondando eficiencias del 23%, por lo que aún se encuentran muy alejados de la eficiencia teórica.

¿Qué tecnologías son las que mayor eficiencia tienen actualmente?

La tecnología más utilizada en la actualidad es la basada en silicio Monocristalino PERC. Esta tecnología ronda eficiencias máximas del 22%. Sin embargo los paneles solares que presentan mayor eficiencia son los basados en tecnología TOPcon y más aún los paneles solares IBC N-type.

¿Existen otros tipos de paneles solares de nueva generación que mejoren los actuales?

Están desarrollándose nuevos paneles solares que incorporan capas de perovskyta y otros materiales para superar la eficiencia media de los paneles solares. Sin embargo, son paneles solares que están en fase de laboratorio y no se espera que se comiencen a comercializar a corto plazo. Por lo tanto, debemos recurrir a los tipos de placas solares que se comercializan actualmente y esperar que las nuevas tecnologías estén maduras y lleguen al mercado.

Conclusiones sobre el límite de Shockley-Queisser:

Como hemos visto, si bien el límite de Shockley-Queisser se establece en un 33% para células fotoeléctricas, y menos aún en aquellas basadas en silicio, se está investigando para desarrollar células multicapa, o multiunión, para incrementar progresivamente los niveles de eficiencia.

Será cuestión de tiempo comenzar a ver paneles solares con eficiencias por encima de ese 33%, pero, hasta ese momento, debemos seguir conformándonos con los paneles solares actuales y sus eficiencias cercanas a su límite físico.

Autor / Redactor: